charging of capacitor" width="289" height="220" />Here derives the expression to obtain the instantaneous voltage across a charging capacitor as a function of time, that is V (t).
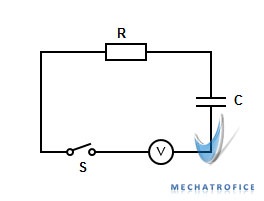
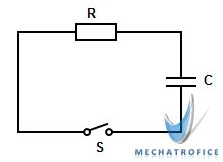
Consider a capacitor connected in series with a resistor, to a constant DC supply through a switch S.
charging of capacitor" width="289" height="220" />
‘C’ is the value of capacitance and ‘R’ is the resistance value. The ‘V’ is the Voltage of the DC source and ‘ v ‘ is the instantaneous voltage across the capacitor.
When the switch ‘S’ is closed, the current flows through the capacitor and it charges towards the voltage V from value 0. As the capacitor charges, the voltage across the capacitor increases and the current through the circuit gradually decrease. For an uncharged capacitor, the current through the circuit will be maximum at the instant of switching. And the charging currents reaches approximately equal to zero as the potential across the capacitor becomes equal to the Source voltage ‘V’.
Capacitor charging equation derivation steps,
Considering voltage law, the source voltage will be equal to the total voltage drop of the circuit.
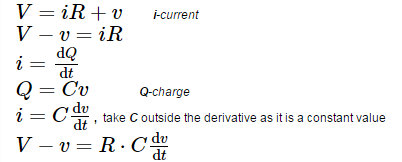
Rearrange the equation to perform the integration function,
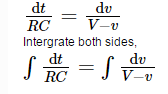
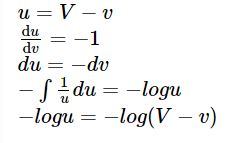
On integrating we get,
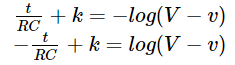
As we are considering an uncharged capacitor (zero initial voltage), the value of constant ‘K ‘ can be obtained by substituting the initial conditions of the time and voltage. At the instant of closing the switch, the initial condition of time is t=0 and voltage across the capacitor is v=0.
Thus we get, logV=k for t=0 and v=0.
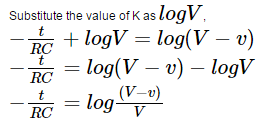
Taking exponential on both sides,
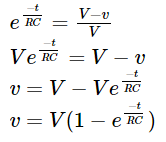
From the above expression, it is clear that the instantaneous voltage will be a result of factors such as capacitance, resistance in series with the capacitor, time and the applied voltage value.
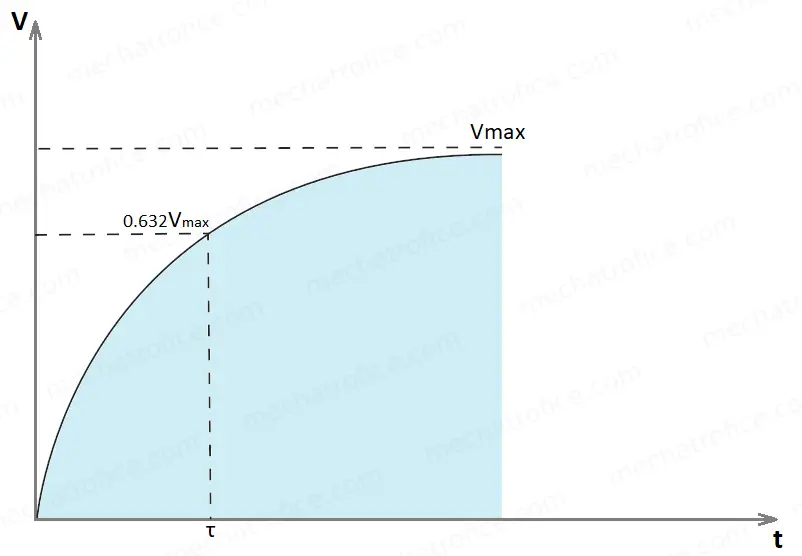
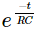
As the value of the constant RC increases, the value of exponential function also increases. That is the rate of voltage rise across the capacitor will be lesser with respect to time. That shows the charging time of the capacitor increase with the increase in the time constant RC.
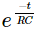
As the value of time ‘t’ increases, the term reduces and it means the voltage across the capacitor is nearly reaching its saturation value.
The expression for the voltage across a charging capacitor is derived as,
ν = V(1- e -t/RC ) → equation (1).
V – source voltage
ν – instantaneous voltage
C– capacitance
R – resistance
t– time
The voltage of a charged capacitor, V = Q/C.
Q– Maximum charge
The instantaneous voltage, v = q/C.
q– instantaneous charge
q/C =Q/C (1- e -t/RC )
q = Q (1- e -t/RC )
For a capacitor, the flow of the charging current decreases gradually to zero in an exponential decay function with respect to time.
From the voltage law,
ν = V(1- e -t/RC )
ν = V – V e -t/RC
V – ν = V e -t/RC →equation(2)
The source voltage, V = voltage drop across the resistor (IR) + voltage across the capacitor ( ν ).
V = i R + ν
V – ν = i R
Substitute V – ν = i R in the equation 2.
Therefore, i R = V e -t/RC
i = (V /R) e -t/RC
As V is the source voltage and R is the resistance, V/R will be the maximum value of current that can flow through the circuit.
V/R =Imax
i = Imax e -t/RC
For a discharging capacitor, the voltage across the capacitor v discharges towards 0.
Applying Kirchhoff’s voltage law, v is equal to the voltage drop across the resistor R.
The current i through the resistor is rewritten as above and substituted in equation 1.
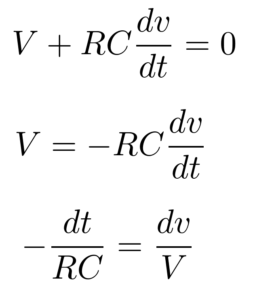
By integrating and rearranging the above equation we get,
Applying exponential function,
The instantaneous voltage across a discharging capacitor is v = V e -t/RC
Instantaneous charge, q = Q e -t/RC
Instantaneous current, i = – Imax e -t/RC
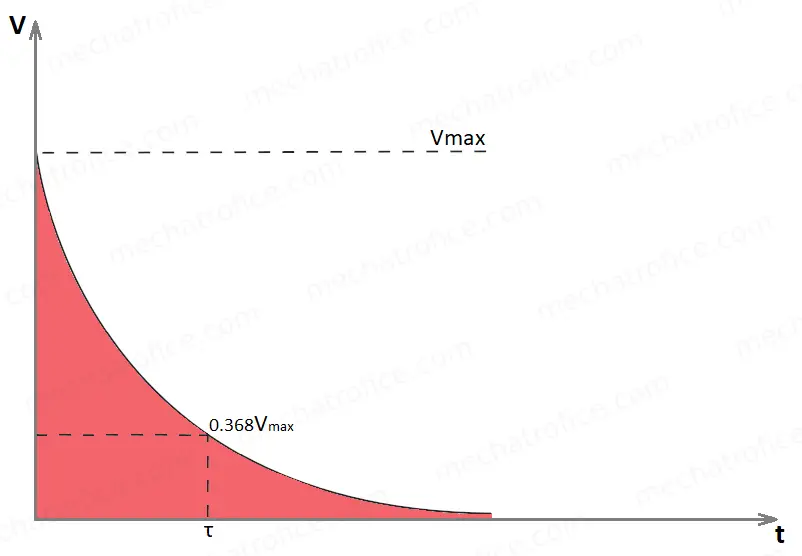
From the above equations, it is clear that the voltage, current, and charge of a capacitor decay exponentially during the discharge. The discharge current has a negative sign because its direction is opposite to the charging current.
